２００７／０５／０３（木）
　「ブッダ論理学　五つの難問」：石飛道子：講談社選書メチエ　に　提起された　二項命題の論理　部分を　図解した。
・Ｐ、Ｑの　命題を　入力したら　論理結果　が　真実・Ｔ　か、偽・Ｆか　どうなるか？入力状態の　１から４までに　対して
　それぞれの　論理で　答えの　出方が　ことなる。
・図書には　図解が　ないので、図を　作成した。
・まず、じっくり　真理値表と　図を　見比べる。それぞれの　論理は　かならず　正・Ｔと　負・Ｆの　出力が　あり、
　論理図も　それに　対応して　２種類ずつ　表記した。　

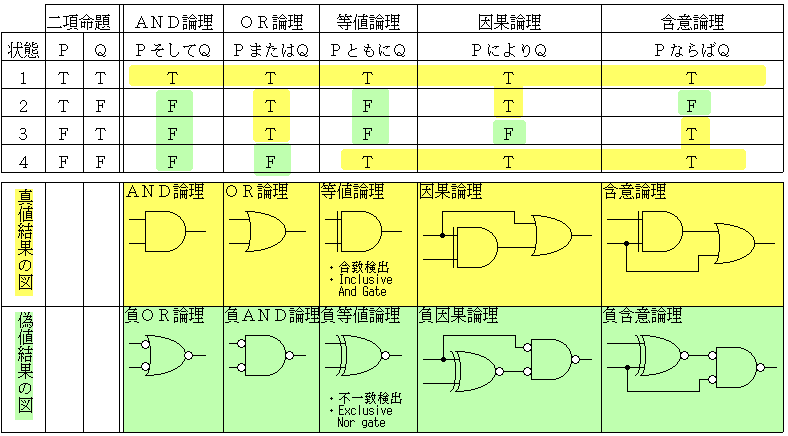
○等値／負等値論理の　場合、等値論理図：Ｉｎｃｌｕｓｉｖｅ　ＡＮＤ　は　３０年ほど前に　私案した　もの。
　当時は　Ｅｘｃｌｕｓｉｖｅ　ＯＲ図のみ　が　一般的に　通用していた。正と負の　相補関係を　満たすために
　包括的ＡＮＤゲートの　図を　考案した。（当時、日経エレクトロニクス・「私の設計」に掲載された）
○等値／負等値の　論理ゲート図を　使えば、因果論理、含意論理も　簡単に　図示　できる。
○因果関係を　論理思考する　には、時間順序が　逆転（：命題Ｑがさき、命題Ｐがあと）する　論理で
　破綻しない　ように、注意深く　命題設定する　必要が　ある。
○このため、ブッダ論理では　状態１と４で　真となる　ように　二項命題を　導き出して　いる。
　（等値／因果／含意の　論理は　安定的に　状態１、４が　真となる。また、Ｐ命題を　原因、Ｑ命題を
　　結果に　あてる　ような　論理立て　だった？）
○論理図解を　試した　だけ　なので、わたし　としては　教典命題での有効性を　示す　段階に　ない。

　・念のためを　追記した。